
This article presents a bibliographic review of the gravitational model in international trade from when it was first associated with Newton's law of universal gravitation. Firstly, I will introduce the concept of gravity in commerce as originally intended by Isard (Q J Econ 68(2):305–320, 1954) in relation to Tinbergen and Tobler’s approaches. Secondly, I will analyse the theoretical roots of international economics according to several authors, including McCallum, Anderson and van Wincoop, Krugman, Tranos, and Nijkamp. Thirdly, attention will be drawn to the evolution of the ideas of the authors mentioned above upon Isard’s initial approach rooted in physics. Furthermore, I will focus on how the tool rooted in physics can be applied or adapted to international trade. Throughout this article, I will try to keep the econophysical nature of this model.
Avoid common mistakes on your manuscript.
This paper aims to examine the gravitational model and the usefulness of this theoretical approach in international economics. The methodology used follows a detailed historical analysis of the literature on the origin and chronological development of this vital instrument, beginning with Isaac Newton's initial formula in physics and concluding with its most current applications. Therefore, the paragraphs follow a chronological order, which is the most appropriate for describing the interdisciplinary development of the physical model. It is worth noting that the element of novelty consists in the suitable combination of the sequential scheme, where the paragraphs are organized thematically and chronologically. To sum up, the organization of the paragraphs follows a historical evolution and a thematic division, that provides a better comprehension and facilitates the gradual discovery of the topics covered. Whilst, in the last 30 years, the topic has been extensively investigated and reviewed, by authors such as Philbrick (1973), Anderson (1979a, b, 2011), Yotov et al. (2016), Head (2003), Carrothers (1956), the present study represents a step forward. Indeed, this research offers an updated and detailed analysis with a broader range of the existing applications of the model. While filling a void in the academic panorama, the study is suggesting an improved thematic division of the gravity model applications to economics and its econophysical evolution.
Contributions applying the concept of gravity are examined, ranging from those describing the movement of people (Ravenstein 1885; Stewart 1947; among others) and those that determine the trade flows (Isard 1954; Tinbergen 1962) to more modern applications. An in-depth analysis of the consistency of gravity of trade with the main theories of international economics is carried out. More specifically, the author investigates the notion of gravity as initially defined by Isard (1954) in relation to the various approaches of Tinbergen's conventional gravity model and Tobler's first law of geography. It takes up the contributions of Isard (1954) and Tinbergen (1962) and argues that Isard’s is more analytically based on the concept of gravity borrowed from physics. On the contrary, Tinbergen, generally considered by literature the forerunner of the gravitational model of international trade, proposes a formula which is a simple basis for the econometric estimation of bilateral trade flows between two countries; an empirical tool that, at most, metaphorically echoes Newton's law without representing a true analytical transposition to the level of ecophysics. Therefore, pursuing its object of research, this work provides a comparison between a simple spatial framework of three variables (Tobler), of which the most important is distance, a simple bilateral trade flows model (Tinbergen) and a structured scheme using the gravity metaphor that incorporates the concepts of attractions’ forces, as well as spatial concentration (the proper gravitational model) as outlined by Isard himself. The issue of the priority of Isard (1954) over Tinbergen (1962), which unfortunately most economists and articles of the field have erred or ignored, is then resolved. Therefore, the key evolutions of the model were studied based on their usefulness, adjusting the deviations according to an econophysical perspective. The latter is more consistent with Newton's theory and its initial applications to demography and economics made, respectively, by Stewart (1947) and Isard (1954). Although the gravity model has been extensively used in numerous empirical research and other economic models, its theoretical underpinnings are still econophysical. The author seems to be particularly sympathetic to the last-mentioned scholars and, more specifically, to Isard's ambition to focus on a multilateral model of the interaction between economic forces and the attempt to merge theories of location choice with theories of trade. It should be highlighted that the gravitational model, as will be made clear throughout this study, is not just a model of flow but also of the interaction of trade forces and spatial concentration. On the other hand, Tobler's model has been used as a reference point for models that depart beyond physics and it is essential to understand the theoretical development of the model in social sciences. In fact, despite being inspired by gravity models, Tobler’s Law is more general and represents purely a distance decay law in geography.
The paper goes on according to the question of research by analyzing the theoretical roots of international economics as defined by various authors following Tinbergen up to the most recent ones. It will be investigated how the physics-based tools can be applied to the social sciences, trying to maintain the econophysical nature of the model. According to this critical approach, the paper will explore and take into account the main developments of the gravitational model as described by authors such as McCallum, Anderson and Van Wincoop, Krugman, Tranos, and Nijkamp. Hence, it can be stated that the main contribution of the article is to the historical field.
Following Isard's viewpoint, the most convincing attempts in the economic literature to develop a multilateral gravitational model are analyzed. The study of the original model lays the foundation for an econophysical critique of the multilateral developments that took place in the trade model. The theoretical underpinnings of the international economy as defined by numerous authors will then be examined. Among these, greater emphasis will be placed on the concept of remoteness as well as the multilateral resistance factors of Anderson and Van Wincoop (2003). Although the notion of gravity in physics is multilateral, it has mostly been employed in economics in accordance with Tinbergen's (1962) standard formula, which describes bilateral trade between two countries. The multilateral approach was later adopted by Krugman (1991), who formulated the New Economic Geography, and McCallum's study of border effects (1995). As we will see Krugman's model recalls many elements of the Isard’s one. These attempts, however, do not constitute a direct evolution of Isard's original multilateral formula, but rather a multilateral implementation of Tinbergen's standard bilateral formula. In short, there is definitely little literature on econophysics in the prevailing econometric method that various authors have followed after Tinbergen's work. Moreover, this produces a variety of challenges, both new and old, even in the international economic model.
Among the applications of gravity law to social sciences, those related to trade have undoubtedly been the most prolific. Hundreds of economics research studies have employed the gravity equation and its solid theoretical foundations to investigate the determinant of international trade. The framework known in economics as the “gravity model” is a theoretical approach that may explain and predict trade flows based on two components: the gross domestic product (GDP) and the distance between countries. As will be seen, the gravitational model has a flexible structure that encompasses multiple market forms and can be used to assess the impact of various commercial policies. It is commonly applied in empirical work on bilateral exchanges between countries because of its predictive power in estimating exchange flows between countries (Head and Mayer 2014).
According to Isard (1954: 308), “the distance variables act in much the same manner with respect to the social world as to the natural world”. As a result, any model that takes distance as a direct component that suggests costs must incorporate a gravitational link. Carrothers (1955: 99) drew a parallel between human interaction and Newtonian physics of matter. Even though “it may not be possible to describe the actions and reactions of the individual human in mathematical terms” the behaviour of a group of people was foreseeable due to the study of probability in mathematics. As stated by the author, this phenomenon has been noticed in all social sciences because people behave differently in groups than they do as individuals. Likewise, in physics, it was impossible to describe the behaviour of individual molecules, but it was conceivable to predict the activity of a set of them. The logical considerations just mentioned, particularly those of Comte (1854), Isard (1954), and Carrothes (1955), are required premises for developing physical reasoning in social sciences, and without which a gravitational sociophysical structure would make no sense due to a lack of logical coherence. In some ways, one can choose whether to believe that human actions are regulated by universal rules or not. Nevertheless, beyond the solution to this complex dilemma, to use a gravity model in social sciences, one must accept a certain level of determinism in human life.
The gravitational trade model naturally predicts commerce between partners using a metaphorical interpretation of Newton's universal law (countries, regions, or companies). In physics, any particle of matter in the universe attracts any other particle via a gravitational force that is directly proportional to the product of their masses and inversely proportional to the square of their distance apart.
Newton's Law, when applied to international trade, implies that, just as particles attract each other in proportion to their size and mutual distance, partners’ trade in proportion to their respective economic size and mutual distance (“frictions of the distance”).
In physics, the formula of Gravity from ground up is the following (Schutz 2003, pp. 13–18):
$$where \(F\) is the attractive force, and \(M\) are the masses (mass i and mass j), \(D\) is the distance between the centres of the two objects, \(G\) is a universal gravitational constant.
Based on the gravity model, international trade flows positively correlate with market sizes. For this reason, when applying the formula to international trade, the economic dimension must be considered first. For states, GDP provides this function. Besides increasing GDP, a nation's sales of goods and services increase the number of services its citizens can import. Further, distance is determined by geographical and spatial factors, including trade barriers. The second factor is distance, which takes into account the geographical and spatial aspects, including trade barriers. Distance affects travel costs and the ease of establishing contacts, which in turn affects communications, which in turn affects trade. Economic size is generally considered a push, while distance is a pull.
On the basis of the considerations above, the application of the gravity model to international economics can be summarized as follows:
$$where \(_\) indicates the value of trade between two countries (country \(i\) and country \(j\) ), \(C\) is a constant, Footnote 1 \(_\) is the GDP of country \(i\) , \(_\) is the GDP of country \(j\) (sometimes even the GNP is used). Footnote 2 Finally, \(_\) is the distance between the two countries. Using the gravity model as an estimation of the flow of international trade also implies the application of geographical factors.
The major problem with the gravity model is estimating the resistance component. Of course, numerous variables other than distance influence transit costs. Using distance as a crow's route may result in the loss of vital information. To address this issue, Hummels (1999) replaced crows' paths with real distance, while Limão and Venables (2001) assessed the effect of infrastructure quality on transportation costs. Based on the approach created by Mayer and Zignago (2005), the distance between countries is measured in kilometers and reflects the distance between pairs of cities, weighted by the proportion of the country's population that resides in each city. Geographical distance is used as a starting point, and it is enhanced by a variety of modifications designed to account more economic, cultural, social, technological, linguistic, and other characteristics. As the opposite of distance friction, these methods occasionally use proximity instead of distance (Torre and Wallet 2014). The choice to consider a straight-line distance or an alternative method of transportation has an impact on the geographic distance measurement, as do other variables that may relate to the locations of the origin and destination. Considering the potentially vast physical region that many nations occupy, as well as the fact that commerce and economic activity occur across a multitude of their boundaries. The most popular databases, USITIC and CEPII, take geographic distance into account. This includes population-weighted distances between countries and distances that represent the spatial distribution of activities inside a country. But also, many proxies for cultural proximity as language, religion, origins of the legal system, colonial ties, etc. This historically ties with the fact that Tinbergen's study group was the first to use colonial, postcolonial, religion, and other cultural and social parameters in a trade model, which is related to the fact that Tinbergen (1962) developed the best-known and most widely applied formula for the gravity model, which was formalized later by his student Linnemann (1966) in his thesis. This is done in an effort to more precisely measure the distance that international trade must cover. The estimated coefficient for the distance variable is significant and has a negative sign. Similar to Herrera's conclusion (Gómez-Herrera 2013), which has depicted any transport cost or trade obstacles that might prevent trade flows. Therefore, if we build a gravitational field across this non-geographic distance, it will spread across these same economic distances in a virtual and not real space. In this sense, in these cases, the term “distance” does not refer to an actual distance measured in meters but rather to a dimensionless quantity (also known as a “pure quantity”) that measures the resistance of distance in the gravitational model of trade. Or rather it should be measured in economic distance meters. Therefore, in these empirical studies and in some gravitational model’s databases, we are not considering the absolute distance between countries expressed in meters, but a relative economic distance whose value depends on the comparison between the distances of other countries. At this point, the use of a weighted or network graph with vertices and edges, which considers the economic distances between states or regions, could be more appropriate. This solution could be effective, since state to state or state to region distances would be more of interest to economists than the distance of any other point in space. On the other hand, the exclusive use of geographical distance would allow an easier representation on a bi-dimensional map. The Newtonian gravitational approach directly implies the specification of the power function, which suggests elasticity at constant distances. However, under a multilateral system, the relative impact of other countries or regions on a trade system could be omitted. Therefore, there are many applications outside trade analysis that use exponential distance decay functions where the elasticity could be affected by distance. The essential difference is that an exponential function has its variable in its exponent, but a power function has its variable in its base. These alternative forms are particularly used in geography and regional sciences (Östh et al. 2016). Due to the function's power nature, changes in distance friction also affect trade volume in a proportional manner. Through model fitting and posterior contrast with dimensional extinction on current assertions, various ways lead to varying power constants. Most studies in economics ignore the square of the distance, which in physics implies a precise verifiable empirical relationship between different measuring systems (system of units) for masses, distances, and forces. The square can be omitted in economics since the value of distance, which is calculated through estimates, is not geographic but economic. The principle is theoretical in social sciences, and its empirical application is dependent on the proportionality between the members of mathematical equality (in the formula), and thus on the practical estimation of distances.
Indeed, the type and number of variables considered in the distance estimation approach are arbitrary in comparison to GDP and exchange flow (F), which are clearly characterized based on a certain currency.
After developing a method (measurement system) for estimating distances in trade, it may be important to determine the accuracy of the square of the distance. The square of distance, however, is still present in some authors.
It is worth noting, for instance, that the square of the distance has a consistent value in Stewart's applications in social sciences, from which Isard took inspiration for his model. In fact, the scholar distinguished between a demographic force ( \(_=k \left(\frac__>_^>\right)\) ) and a demographic energy ( \(_=k \left(\frac__>_>\right)\) ), thus employing the square of the distance. In social sciences, this principle is theoretical, and its empirical application is influenced on the practical assessment of the distances, which in turn are given by the proportionality between the members of mathematical equality (in the formula). In fact, while for the distance determination method, the type and number of variables considered is not systematic, the measurement of GDP and exchange flow (F) is measurable through a given currency and thus, univocal. When an evaluation method (measurement system) has been established for trade distances, I recommend evaluating their square of distance accuracy. In Anderson's view (2004: 334), the theory that human behavior varies non-linearly, but with the square of a given variable, has proved “strong and resilient” over time. The square is used in a variety of works in social sciences. For example, Malthus forecasts ongoing problems with the geometric growth of the human population in relation to the arithmetic growth of necessities. In 1890, the father of regression, statistician and sociologist Francis Galton understood that for the mathematical use of the square of the deviation, “there seems to be a wide field for the application of these methods to social problems” (Galton 1890).
Nonetheless, since the application of the law of gravity to the social sciences, the concept of a squared exponent of distance has only sometimes been applied. It was rather maintained a gravitational structure that takes into account the attraction force (often referred to as 'magnetism') of a considered variable mass and a more generalized use of friction or distance resistance based on the specific phenomenon in question (Sen and Smith 1955). However, this is only true for some researchers, as shown by Stewart's (1941) approach, which places theoretical emphasis on the square of distance.
To sum up, the gravity equation can be conceived as a representation of the main forces that affect international commerce demand and supply. If the country is the origin, then it represents the total amount that can be provided to all customers and represents the total destination of the demand. As a result, distance, which is inversely proportional to the commercial flow between countries, acts as a sort of ‘wedge’ tax imposing commercial costs and influencing choices. Therefore, GDP plays the role of physical mass in attracting trade flows between two countries. It follows that the greater the GDP, the greater the volume of trade that occurs. The resistance factor includes all variables acting as trade barriers that negatively affect trade between countries, including distance. This is used as a measure of transportation costs in most studies.
Van Bergeijk and Brakman point out that the gravity model and its earliest systematic and scientific applications to social sciences dates back to the nineteenth century. First, Carey (1858, p. 42) applied Newton’s universal law of gravity to “railway traffic and migration” by tracing a tendency for the individual to “gravitate to his fellow man”. According to the scholar, the individual, as a component of society (‘molecule of society’), is subject to a force of social attraction to other social agents, just as matter in physics is subject to a force of gravitational attraction with other matter. An early cogent formulation of the gravity narrative is Ravenstein’s (1885, pp. 198–99), who explains how "currents" of migration are driven by the "absorption of centers of commerce and industry" but "grow less with the distance proportionately". Above all social interactions, the gravity research for immigrant flows was the first to be conceptualized. Early research focused on applications to flows of people rather than movements of things. In urban geography, the gravity model is used to assess traffic patterns, migration between two places, and the attraction of people to a center or to several centers. Many factors, including politics, language, culture, taxation, and others, affect how far individuals perceive a distance or the attractiveness of an area. These characteristics are influenced by free trade agreements and, more broadly, by population movements.
Ravenstein (1885) defined this notion in migration law, stating that a “populated center” draws migrants from other “populated centers” in proportion to population size and inversely linked to distance between centres. The mathematical function is as follows:
where \(_\) is the migration flow from centre j to centre i, \(f\left(_\right)\) is a function of population size i and \(_\) is the distance between the two population centres.
Later, Reilly (1929) extended the concept of social gravitation to consumers and cities. The author illustrates how the city’s force of attraction exerted on nearby customers is directly proportional to the size of the population and inversely proportional to the square of the distance between the two. Therefore, ceteris paribus, larger cities will be more appealing to customers than smaller ones. Nonetheless, in accordance with Newton’s law, at the specific ‘breaking point’, consumers will be indifferent to either of the two competing cities, as demonstrated in the following formula (Reilly 1931):
where \(_\) and \(_\) are, respectively, the size of the centre i and the centre j, \(_\) is the distance of the indifference point from the centre i and \(_\) is its distance from the centre j.
The astrophysicist John Q. Stewart (1941) applied the laws of physics to the study of social sciences, laying the theoretical groundwork for further research in social physics. The researcher realized that the law of gravity might also be used to describe demographic phenomena when studying empirical regularities linked to distance in social sciences.
To that purpose, the author employs the notion of demographic gravitation, which states that many people, such as the population of a big city, act as a force of attraction for other individuals who eventually choose to migrate there. The following is the formula:
where \(_\) is the interaction force between the demographic centres i and j, \(k\) is a constant, \(_\) is the population of the area i, \(_\) is the population of area j, and \(_\) is the distance between i and j. Footnote 3 More specifically, Stewart proposed to adopt different values for the population by nationality, considering the ‘molecular weight’ of each member of the population. The author picked the molecular mass of the average American as a unit to standardize the measurements. The latter, for example, will be distinguishable from an Australian aborigine, whose molecular weight will presumably be less than one.
Taking into consideration the vector property already mentioned, this can also be expressed at point i as (Philbrick 1973, p. 42):
where \(_\) is the population's potential for attraction to centre i, \(K\) is a constant, \(_\) is the population of all other areas in the particular universe under consideration, and \(_\) is the distance.
In several studies, the astrophysicist proved how the outcome of his formula might be utilized to draw a map of the surface using the device of ‘contours of equipotential’. The latter is akin to a ‘synoptic weather chart’, as demonstrated in Fig. 1 produced by Stewart. This is also clear from the fact that formula (15) is analogous to and derives from the formulas of gravitational fields (6) in physics. The graphic depiction takes on the features of a gravitational or magnetic field, complete with its equipotential contours.
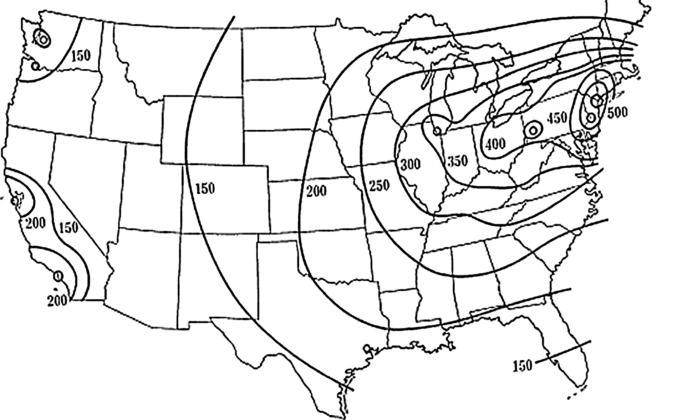
Gravity is used in the study of migration, demographics, and journeys, as well as in the study of international trade. Stewart's model has had a direct impact on the economic model, which replicates its logic and dynamics, but it transposes gravity to a flow of commerce rather than to a stream of people. The application to the study of international trade traces back to the work of Walter Isard (1954), but it was popularized in Tinbergen’s (1962) standard bilateral form, which was directly related to Newton’s Law of Universal Gravitation. Subsequently, several economists revisited it. Isard was inspired by Stewart’s model and introduced the concept of income potential. Thus, the author applies a gravitational field equation in physics to the study of international trade.
We will now be moving on to the analysis of the gravitational model in international economics, starting from Isard’s and Tinbergen’s studies, which have been mentioned in the first section. Contrary to what has been erroneously reported and inferred in most research papers, Tinbergen (1962) was not de facto the first one to use the gravitational laws of physics in international trade. Footnote 4 Indeed, the application of the gravity model to social sciences was quite common in the second half of the last century (Stewart, Zipf, Vining, Ullman and others), and Isard was the first to suggest its application to international economics in 1954.
Although he has never made a comment regarding authorship, Tinbergen's name is regularly associated with numerous laws and models. For some reason, the Dutch scholar was quoted. These quotes were mentioned again, and whenever something he said was linked to a theme, it became a law or a rule.
As part of his academic activities, Isard focuses on multiregional input–output frameworks, the gravity model, potential models, game theory, interregional programming, complex industrial analysis, conflict resolution strategies, environmental and ecological analysis, and more.
This multiregional approach led Isard to become one of the main founders of regional science and peace science in economics. His handbook Methods of Regional Analysis: an introduction to Regional Science, which was the first book in use in Regional Science, contains empirical methodologies he elaborated through the years, either alone or with his collaborators. Since he was a student at Harvard, under the supervision of Alvin Hansen and Abbott Usher, Isard was interested in location issues. After his employment at Harvard, together with Capron, he published a classic paper on the location of the U.S. iron and steel industry in 1949, followed by Location and Space Economy (Isard 1956). So, it can be said that he pursued his interest in regional science and localization theories from an early age (Boyce 2003) and aimed to develop, in his words, a "superior set of tools" (Isard 1954: 305–320), culminating in the dream of developing an improved theory of trade and regional phenomena.
This single general theory summarized three broad theoretical perspectives, starting with international trade, the Walrasian’s notions of general equilibrium and the concepts of location, in which the key elements were distance and transport inputs. Isard believed that “a general and comprehensive location theory and a general and comprehensive trade theory are one and the same”. This integration affects both the long-run and short-run analyses. In the long-run analysis it does so by combining the notions of “distance inputs transport orientation” and of opportunity cost to yield a superior set of tools (Isard et al. 1969: 319).
In the short-run analysis a considerable development of the two theories of trade and localization is necessary to perform a fusion. For this purpose, Isard proposes a multilateral analysis through the gravitational instrument (Isard et al. 1969). According to the scholar (1954), distance and transport factors were still being undervalued in international trade studies: he assessed that since transport inputs are not flows from a stock like capital inputs, they must not be treated as a factor of production. Referring to Weber's previous theories, he acknowledged that their treatment as intermediaries was more appropriate. According to Weber, the classical theory of commerce fails to take into account the significant proportion of industry that is transportation-oriented, and he aspires to a more comprehensive theory that incorporates transportation costs (Weber 1911), and Ohlin, who endorsed Weber’s approach and thought that the theory of international trade was only part of the localization theory, he argued that excluding the distance component would mean restricting oneself to an unrealistic world (Isard and Peck 1954: 114). Only by merging trade with geographical space through localization theories, it would be possible to develop a greater theory in the field of international economics. Consistent with these assumptions and inspired by Newton’s universal gravity, Isard introduced a functional law to analyse international trade flows. At the heart of his theories lies the idea that geographical proximity promotes trade, because of the several underlying reasons, ranging from low transport costs to institutional and linguistic similarities between states. Therefore, he concluded that a gravitational relationship must arise in any model that considers distance to be a direct factor in increasing costs. Footnote 5 According to Isard (1954), the resistance effect of distance acts in a similar way in the social world, if compared to the natural world. Indeed, the economist himself stated that “the distance variables act in much the same manner with respect to the social world as to the natural world” (Isard 1954: 308). Indeed, Isard, inspired by the socio-physics approach of Carey (1858) and Stewart (1941), thought the human being as a “molecule of society” that “gravitated to his fellow man”; thereby allowing scholars to use newton's laws of physics also in social sciences. He drew on Stewart’s notion of demographic gravitation (1941), a concept that, along with “demographic energy” and “potential of the population”, forms the foundation of his theories, creating the structural basis for later studies in social physics. The key concept is that human beings behave as a whole of molecules of society: the population of a city, for instance, acts as a force of attraction for other people, who will be attracted by its potential and will decide to migrate there). Isard took it up from Stewart’s earlier study, as highlighted by Fig. 1, to re-propose it in his 1954 book to explain the concept (1947) of ‘income potential’ in international economics, according to the following formula (Isard 1954: 308):
$$<>_<>V= \sum_^<>_<>_=\sum_^k\frac_>_^>,$$\(_\) is the income of nation (region) \(j\) , \(_\) is the average effective distance (that is distance adjusted for level of transport rates) between nations \(i\) and \(j\) , Footnote 6 \(a\) is a constant power to which \(_\) is raised, \(k\) is a constant similar to the gravitational constant, \(iV\) is the income potential produced by nation \(j\) upon nation \(i\) , and \(iV\) is the income potential produced by all nations upon nation \(i\) .
In Isard’s formula, the income potential, produced by a given nation on nation \(i\) , varies inversely with the intervening distance. Between two nations similar in resources and technological development, the closest to nation \(i\) will have a greater income potential on \(i\) .
Isard's formula (7) is multilateral, since it considers the effect on the income of nation \(i\) caused by the change in wealth of a sum of countries, considering the friction of their distances. Footnote 7 Furthermore, according to the scholar (Isard 1954: 318–320), this formula would become over time an instrument for a complete and superior synthesis between the theory of localization and international trade. Before Isard, Ohlin (1933) faced the same problem: he stated it was necessary to demonstrate that the theory of international trade is only part of a general theory of localization. In order for spatial and price aspects to be considered simultaneously, economic geographers and economists should collaborate. According to economists, it is also necessary to analyse the movements of goods in relation to the movements of factors of production at national and international levels. It should be noted that Isard and Ohlin had been inspired by Weber's ideas (1911), according to which the classical theory of commerce overlooked "the significant amount of industry that is transport-oriented".
In 1962, Tinbergen and his students developed the traditional mathematical equation of the gravity model used for trade (2), and applied it empirically for the first time to the study of international trade in the work Shaping the World Economy. Moreover, in his original estimate, he predicted positive signs for the coefficients of economic attractors and negative signs for the distance. The in theory predicted a coefficient that could also be negative in the case of self-sufficiency. However, he was more interested in the empirical aspect, and every country he analysed a positive coefficient. We discussed "expected signs" in the gravitational model's regression because later studies confirmed the sign of the coefficients: positive for economic size and negative for distance. He also argued that the size of the economy of the importing country plays a dual role, indicating both total demand (internal and external) and the degree of diversity of production.
Tinbergen obtained a doctorate in Physics from the University of Leiden in Netherlands, and he was the first Nobel Laureate in Economics with Ragnar Frisch in 1969. His passion for these two disciplines led him to study international trade and to apply Newton’s gravitational law to economics studies. His model appeared in the appendix of a semi-popular book that discusses a new economic ordering for the world, without references, and this could explain why there is none related to Isard’s work.
While Isard was the first scholar to bring gravity into the analysis of trade flows, Tinbergen is considered the pioneer of the standard gravitational formula (2) which, stemming from Newton's gravitational law, (1) creates a simple and intuitive bilateral model for the empirical analysis of trade between pairs of countries. While Isard was looking for a complete theoretical approach for an all-inclusive analysis, Tinbergen was more interested in the empirical aspect. Footnote 8 Isard's gravitational instrument was created as part of a more exhaustive analysis of the international economy. As previously seen, whatever trade theory is considered, progress can only be achieved by combining international trade with economic geography via space and localization theories. The goal of this fusion is to create a superior set of tools and a conceptual framework for empirical and theoretical regional analysis. Isard develops the concept of income potential to avoid the customary but unrealistic two-country analysis and to consider the impact of the distance variable on trade and income in an aggregate and multi-country framework.
Tinbergen supervised Linnemann's thesis, which is now considered the canonical reference for the early gravity equation formalization. Probably, the model was chosen for describing the worldwide network of bilateral commerce, especially in terms of political ties. Tinbergen was motivated to move into economics by development issues and social policies. Indeed, throughout time, he started to stress the need for science to have an impact on society. He considered this crucial in an era where humans had failed to see the inevitable consequences of technology, of the psychosocial pressures to which they were subjected, of their exploitation of natural resources, and of the environment’s pollution. This was due to “our one-sided appreciation and our complacent acceptance of the blessings of our civilization, of reduced infant mortality, of increased affluence, of our “spiritual life” and last but not least of science itself” (Hinde 1990). Due to the fact that the model credited to Tinbergen is more econometric than econophysical like Isard's, a physics scholar may not often notice his contribution. Not only did Tinbergen use econometrics but he is also considered one of its founders. This is quite fascinating and brings up the duality that was thoroughly covered in this study. In fact, Tinbergen and Ragnar Frisch are regarded as two of the fathers of econometrics. In 1969, together with Frisch, he became the first recipient of the Nobel Prize in economics for having developed and applied dynamic models to the analysis of the economic process. Footnote 9 Isard, on the other hand, is legitimately recognized as one of the founders of econophysics. Therefore, it is worth noting the differences between these two fields of study. The econophysical method is based on the application of the rational logic and structures that characterize the world of physics, whereas econometric solely uses mathematical and statistical tools to construct models to assess the validity of economics hypotheses. In summary, econometrics can be defined as the process of developing economic models using statistical and mathematical techniques. The application of physics-related methods and tools to economics is known as econophysics, on the other hand. The econophysics approach does include econometric tools, but it is not this one that characterizes it.
As it will be seen in the next paragraphs, considering the simplicity of application of the standard gravitational formula and its popularity, this empirical approach has been further developed by subsequent authors. As a matter of fact, these new studies followed Tinbergen’s model, constituting a mathematical improvement and an econometric refinement of the formula. Tinbergen’s model was even applied to different locations, markets, and time frames, ensuring its success in literature, whilst over time moving away from Isard’s econophysics theoretical model and losing value and relevance in terms of the relationships of attraction, magnetism, and differing levels of economic power between various trading partners.
Tobler’s economic model has been applied to the study of international economics as previously mentioned. The Tobler model in economics will be useful here in clarifying the difference between a simple distance decay trade model and a true gravitational trade model. By definition, the latter will cross the boundaries of trade into other fields of economics such as geopolitics and the economic analysis of spatial concentration. In this sense, it provides a valid comparison between a simple spatial framework based on three variables, with distance being the most significant, and a structural framework based on the metaphor of gravity in terms of ideas of attraction forces and spatial concentration. These forces modify the surrounding reality which, therefore, cannot be static. This confirms that the gravity trade model has a theoretical econophysical structure based on a strong bond between psychics and the economic model. Regarding this link between natural and social sciences, another point to take into consideration is that human interactions are considered through deterministic premises. Footnote 10
As previously mentioned, the Swiss-American geographer Tobler (1970) was also inspired by the use of the gravitational model in social sciences. He formulated his first law of geography in the Journal Economic Geography and applied it to the study of international trade. Footnote 11 (Tobler 1970: 234–240). In formal terms, the formula is (Rey 2001, pp. 9393–9399):
where \(_\) is the degree of spatial interaction (migration, trade flows, air travel, et cetera) between place \(i\) and \(j\) . \(_\) is proportionate to the size of the populations and inversely correlated to the distance. \(_\) is the population of the origin and \(_\) of the destination. \(_\) is the distance between these locations. The strength of the decline in interaction with increasing separation is estimated by \(\beta\) .
The similarity between Tinbergen's standard equation of gravity (2) and Tobler’s first law of geography (8) is evident. However, unlike the idea of gravity, Tobler’s law is more closely related to geography, to distance decay, and to a geometric approach of similarity. Gravity also entails relationships of attraction and economic force between various trading partners, as we have already seen. Furthermore, Tobler’s law was about ‘everything’ and not only measures masses as for the gravity, thereby leaving appropriate room for studying non-material concepts such as knowledge, culture, ideas, et cetera.
As previously noted, Tinbergen’s interest lies primarily in the empirical aspects and in the study of bilateral trade between countries. Further studies were inspired by this approach, as they left aside physical aspects which were originally present in Isard. It is worth recalling that Tinbergen was a physicist and that he was the first Nobel Laureate in Economics, prize won alongside Ragnar Frisch in 1969. This suggests that, besides emphasizing the intense connection between physics and economics and the usefulness of the application of the former to the latter, many economists yet overlook this aspect and the scholar was aware of such link when introducing the equation of gravity in international trade. Although Tinbergen was also aware of the interdisciplinary nature of the model, as his education was more related to physics than to economics, the gravitational model he developed (and later generalized by Tobler in geography) lost its original econophysic connotation over time. Starting with Tinbergen’s formula for estimating bilateral flows, the focus of economics was mainly on the econometric development of the model and its empirical refinement to adapt it to the study of different cases in space and time. Nevertheless, Isard’s original model is not, as previously mentioned, a simple empirical exercise that uses three independent variables to calculate a bilateral flow. This seems to go against the view of many economists with respect to Tinbergen’s equation. Such perspective implies a diminished value of the word gravity itself, which should theoretically characterize this model. It would not make sense to apply the law of universal gravitation to explain only a theory of distance decay that could be sufficiently interpreted by Tobler’s first law of geography, according to which “everything is connected to everything else, but things near are more connected than things far”. Footnote 12 Certainly, this principle is not exclusive to the gravity model: the latter could be read on a spatial dimension and through the principle of contiguity and spatial correlation. However, Tobler's approach, based on this spatial dimension, results less specific since it focuses more on the concept of space rather than on the gravitational model. In fact, strictly related the gravity models is the concept of attractive forces, even in direct competition with each other where economic weight provides attractive commercial power. In short, Tobler's approach describes how a certain effect is diluted as space increases, whereas strictly related the gravity model is the specific concept of commercial force and commercial attraction, which fades as distance increases. Although this law was more related to geography than gravity itself, Tobler (1975) has later demonstrated his awareness of the dimension of physics. Through a detailed analysis of spatial models and flow implicit in a geographic interaction, the scholar used the gravitational model in relation to the gravitational fields generated by it, considering its magnetic potential field. He used a field of vectors computed from the related net exchanges, which explains the flows and approximates the gradient of a scalar potential. The introduction of a flow field, which is typical of physics, could be cartographically represented as a “wind” for the geographer. The concept of field and the equipotential lines already analysed by Isard (1954) and Stewart (1941) before him are then taken up again. In addition, Tobler analyses in a geometric and detailed way how to calculate the latitude and longitude coordinate of positions in this field.
The application of gravity to trade therefore encompasses a more complex structure and logic, composed of economic forces acting in space and principles of attraction, which in this case are commercial and spatial concentration. Footnote 13
As already mentioned, Isard (1954) was the first to apply the laws of gravity to international economics. Nonetheless, in 1962, the physicist Tingerben developed a gravitational model on the influence of distance in international trade with a spatial-level perspective, which became the most influential and famous work in this field. The gravity equation measured trade costs or barriers that were not yet fully considered in the classical theory of international trade. Starting with Tinbergen, the model began to be applied extensively to empirically test different markets. However, this large-scale application was progressively drifting from Isard’s original model based on theoretical econophysics. Based on these considerations, the following paragraph aims at examining the most important authors following a chronological order. This approach is deemed the most appropriate to analyse the evolutions that the gravity model has undergone over time from an interdisciplinary perspective.
Pullainen, Pöyhönen and Linneman’s contribution has been critical since they further developed the gravity equation with an econometric and empirical prospect. The Finnish economists Pulliainen (1963) and Pöyhönen (1963), who were a competing research group with the one working at the Netherlands Economic Institute where Tinbergen was the director, used the gravity equation in their studies. Linneman was part of that group as well. He later became a professor in trade and development, first at the Institute of Social Studies in The Hague and later at VU Amsterdam, where he also followed in the gravity tradition. While Pulliainen considered a gravity model without commodity prices, Pöyhönen developed a gravitational model similar to Tinbergen’s one using a matrix form for the exchange of goods. The latter considered the GNP and the amount of population in a state as “masses”. His model can be summarized as follows (Zhang and Kristensen 1995:309):
$$where \(_\) is the size of a bilateral trade flow, the two \(GNP\) are the two countries’ gross national product, \(_\) is the distance, \(_, _\) are income elasticities of exports, \(_\) is a transportation cost coefficient, \(\alpha 4\) is an “isolation parameter”, \(_\) is an export parameter for the \(^\) exporting country, \(_\) is an export parameter for the \(< \rm th>\) importing country, \(c\) is a constant.
As for Linnemann (1966), he studied the role of distance in international trade, looking for a quantitative explanation of commodity flows. Tinbergen at the University of Rotterdam oversaw his PHD thesis. He extended the gravity model using the Walrasian model, and he classified three categories of costs associated with trade: transportation costs, time-related costs (perishability, et cetera), and costs linked to cultural unfamiliarity (lack of familiarity with law, cultures, customs, and languages, et cetera). Linnemann elaborated the data coming from 80 countries and 6300 bilateral trade exchanges. He found that both distance, which was treated as a proxy, and population size negatively affected trade relations. This outcome was due to the fact that the most populated countries had a larger market and, hence, they were more self-sufficient. Therefore, the scholar's approach was econometrics like his teacher’s, and referring to Isard’s work he stated, “Some authors emphasize the analogy with the gravitation law in physics (…) we fail to see any justification for this” (Linnemann 1966: 34–35). Indeed, he intended to emphasize the lack of empirical evidence in the theoretical physical model, and for this reason, he had calculated that the elasticity of trade flows to distance was not equal to 2. Professor Linnemann creates his own empirical trade flow model. In essence, he develops a model of the interplay between prospective supply and demand for traded products, together with what he refers to as trade-resisting factors. Both natural and artificial barriers to commerce, such as the significant element of distance, tariffs and other commercial arrangements, are included in the latter. It is presumable that country \(j\) 's prospective demand for country \(i\) 's goods will rely on country \(j\) 's GDP and population size. His international trade model can be elaborated as follows (Zhang and Kristensen 1995: 310):
$$where \(EX\) is the bilateral flow, interaction between potential demand and potential exporter’ supply of traded goods, which is dependent to “resistance” to a trade flow as well, i.e. their cost of doing business. In his equation, \(GNP\) is countries' potential demand which is assumed to depend on that country's income or GDP. The two \(POP\) represent the two population size, \(_, _\) are population elasticities of exports, \(_, _\) are income elasticities of exports, \(_\) is an “isolation parameter”, \(D\) is the distance which coincides with the resistance to trade. The latter includes both natural and artificial barriers to commerce, such as the significant element of distance. Artificial barriers to trade include tariffs and other trade agreements. and \(PR\) is the potential preferential-trade factor which aims to strengthen the trade link between \(i\) e \(j\) and it equals to \(\left(PR\right)\) . Population is a crucial element here with respect to formula (10) above. Indeed, unlike GNP, population is included by Linneman at the denominator as a factor of resistance: a larger population reduces trade. This is because GDP per capita is taken into account (the higher the GDP per capita the more trade is promoted) and because an increase in population increases a country's internal trade magnetism. This is because larger countries are better able to be self-sufficient. It is worth noting that it has become clear, especially after World War II, that a country's international trade tendes to grow faster than its GDP. According to Linneman, this is partly due to a growth path in a dynamic equilibrium since new countries are accepted as members almost continuously.
Leamer (1974) used the gravity equation and the Heckscher–Ohlin’s model separately, in a regression analysis to explain variables of trade flows. He added factor-endowment variables, finding that they performed less well than the standard income and population variables. Leamer and Levinsohn (1995) integrated distance and comparative advantage into the H–O model. They argued that, as in the gravitational model, the majority of goods are produced close to the most important economic centres, which are also their destinations, whereas small countries, far from the central development zones, gain a comparative advantage by focusing on goods (such as shoes and clothes) easy to transport.
As previously mentioned, Tinbergen’s bilateral gravitational model became the standard of the gravitational law’s econophysics application to international trade; indeed, Walter Isard's name is not even mentioned in large sections of international literature. This is probably due to the simplicity of Tinbergen's model, its resemblance to Newton's law, and its empirical usefulness in estimating bilateral trade between pairs of countries. For this reason, many scholars have evaluated the nature of the model merely based on the empirical and practical approach that Tinbergen adopted in his model. Thus, the strong stability of the standard gravitational model and its power to explain bilateral trade flows stimulated a ‘new’ theoretical exploration which, however, no longer included Isard's theoretical development. Anyway, it is worth noting that Head and Mayer (Head and Mayer 2014) individuate in Tinbergen’s model a lack of theoretical foundations which represented one of the main weaknesses that led to the limited acceptance of the gravitational model as a central element in the theory of international trade by the majority of scholars. Anderson (Anderson 2011: 134) called the early gravity model “an intellectual orphan, unconnected to the rich family of economic theory. Shahriar et al. (2019: 29), however, made a good point by observing that: “As a result of the previous studies the model, in no way, is an intellectual ‘orphan’ but rather is now connected to the rich family of economic theory”. Indeed, the criticism of the lack of theoretical roots does not consider Isard's theory but limits itself to considering only the developments of the empirical model starting from Tinbergen. The focus is now on guaranteeing that every empirical test of the gravity equation is clearly defined on theoretical grounds and that it can be linked to one of the existing theoretical frameworks given the abundance of models available. As a result, the most recent methodological advancements pointed out the importance of precisely defining the structural form of the gravity equation as well as the consequences of inaccuracy. In this context, the multilateral dimension of the gravity model is a first significant area of contributions.
Anderson (1979a, b) was considered the first to attempt a theoretical derivation of the gravity equation and explain the role of income variables. Footnote 14 Before him, most scholars saw the gravitational model as a fortunate application of physics to economics. Footnote 15 In International trade theory, the gravity equation is one of the most stable empirical relationships, allowing it to accurately estimate bilateral trade flows. Anderson interpreted the gravity model envisioning an approach conducting cross-section budget investigations. There are efficiency improvements to trade off against the bias issues that have recently been shown, especially given how much transit costs vary. According to Anderson's research, due to the complexity of modeling trade flows, the gravity model may deserve more development and use, therefore any potentially effective technique must be respected. Anderson for instance, attempted its application to policy which resulted significantly hampered by its “unidentified” features. There is no theoretical reason for including policy instruments like border taxes in the equation and drawing conclusions about the impact of taxes based on how the equation has evolved over time without accounting for tax changes provides no assurance of correctness.
The price equality of traded goods model by Samuelson-Heckscher-Ohlin had been proven unrealistic for the differentiation effects arising from the borders of countries. Anderson assumed that preferences for traded goods are homothetic and homogeneous across countries. Furthermore, he assumed that goods are to be differentiated based on the country of origin. According to the gravity model, consumers spending on tradable goods is a steady reduced-form function of population and income. Transit cost variables determine the percentage of each tradable good category among areas. The scholar also assumed perfect competition, that consumer utility preference function is a Cobb–Douglas type, the consumer’s homothetic utility function, constant elasticity of substation (CES), a labour only production factor, the absence of trade costs and that each country produces only one particular good that can be substituted with another nation’s goods (Anderson 1979: 106–16). Each country is assigned a particular GDP, avoiding the GDP being the result of an underlying production function. Since trade was separated from traditional causal factors such as technology or factor endowment, Anderson and van Wincoop (2004) used the term “separable trade theory” to describe this approach (Anderson and van Wincoop 2003: 691–751). In their model, economists explain why only a fraction of goods shipped arrive at their destination by including iceberg costs. The rest has metaphorically melted during transport. If imports are measured at the CIF value, of course, transport costs reduce trade flows. As a result, in a condition of equilibrium and regardless of price, every country will consume commodities from any other country and every type of product will be traded internationally. National income will be equal to the sum of domestic and foreign demand for the single commodity produced by each country. Every good other than the one produced in that country will be imported. For this reason, as in the gravitational model, larger countries will have larger trade flows (Bacchetta et al. 2012).
Krugman, (1991) first with Fujita (1999), and then with Fujita et al. (1999), took his previous study with Helpman and Krugman (1985), indeed, through their theory of New Economic Geography, they began to study the effects of economies of scale, business clusters, technological innovation, and the digitalization of innovations. This new theory sought to explain how the variables of economic and geographical distance in international trade influence the phenomena of concentration and distribution of countries’ economic activity. In a world of rising returns and high transportation costs, there will be an incentive to concentrate production of a good close to its largest market. It may be more effective to locate manufacturing in a single place as close as possible to a bigger market to minimize transportation costs. That is why nations would tend to export the products for which they have a sizable local market as it is frequently stressed in location theory rather than trade theory. In this context, high domestic demand for an item will tend to result in an import rather than an export, which would always be more advantageous since it reduces the need for transportation by equalizing the manufacturing costs in both nations. This advantage needs to be counterbalanced by a salary difference to safeguard employee’s employment in both nations. Therefore, considering the transportation expenses, it can be demonstrated that the nations with more significant domestic markets will have higher pay rates. To sum up, nations will tend to export items for which they have sizable domestic markets as legal justification. On the other hand, smaller nations with far smaller marketplaces, must make up for this disadvantage by paying lower wages. The Heckscher-Ohlin theory and what has been explained so far have a link. According to Mundell (1957), trade restrictions like tariffs or shipping costs would prevent factor movements in an H–O environment where factor mobility would be similar.
Therefore, a general equilibrium analysis in trade is provided where factor movements, spatial dimension, and location problems are considered. Since in international economies distance and commercial costs, which affect either the flow of trade or the position of firms, have been mainly studied through the gravity equation, it is not surprising that the empirical studies related to Krugman's theory of New Economic Geography have made extensive use of the calculation of data and of the gravitational instrument. Therefore, the two models have frequently influenced each other indirectly. I do not intend to minimize the attribute’new’ in the proper name New Economic Geography. Krugman's theory certainly enriches the economic subject matter. However, in 1954 Isard, albeit in a different way, had evidently already addressed these topics. This scientific heritage is recognized by Krugman himself, who, with Fujita, quotes Isard (1956). Krugman recognizes his ideas as “a continuation, perhaps even a validation, of Isard's dream of returning space to the core of economics” (Fujita and Krugman 2004: 153). As mentioned, Ohlin (1933) had already faced these problems with the following intentions before Isard. First, he presented the issue of overcoming the need for more attention of economic theory to the localization problems through a collaboration between economists and economic geographers to demonstrate that the theory of international trade is only part of a general theory of localization. Second, through this new perspective, the need to build a theory of international trade in harmony with the theory of prices and independent of the classical theory of the value of labour was highlighted, in which the differences in transport cost and in the supply of factors of production are considered. Finally, Ohlin identified how challenging it was to use this theory to simultaneously analyse the relationship between national and international movements of goods and factors of production. At that time, however, the lack of modelling techniques to combine increasing returns to scale with the analysis of general equilibrium did not allow Ohlin to satisfy these three objectives, which instead have been partially accomplished by the New Economic Geography. Moreover, this purpose of returning space to the centre of the economy is familiar for the gravitational model. Indeed, we have already seen Isard’s attempts to measure the intensity of the magnetism of a centre or a region through gravitational models in the previous discussion on the model’s origins. Furthermore, the economist had argued extensively about the need to arrive at a “superior synthesis between the theory of localization and International trade”. Krugman, for his part, examined business and space by recognizing two forces: centrifugal forces that push companies to compete to satisfy the demand in any market and region of the world, and centripetal forces which, due to increasing returns to scale, account for the agglomeration of companies. The wealthiest and most productive economic regions can attract more companies and workers thanks to economies of scale, knowledge, and migratory phenomena. Hence, the result will be a concentration of production in certain areas. There is a tendency on the part of industries belonging to the same sector to come together, thereby creating a more efficient labour market for companies and workers in that sector. This would benefit specialisation and, consequently, the positive spillover effects.
The study also analysed distances and transportation costs, arguing that these force companies towards locations close to large outlet markets. Moreover, it identified the “home market effect” as the tendency of businesses to operate in the country with the highest consumption of a particular good.
McCallum (1995) used the gravity equation to estimate the influence of national borders as a discontinuity of distance, and he pointed out that the border’s effect is an obstacle to trade. This topic was familiar to the gravitational model in economics or, more generally, to its applications in social sciences. In 1948, astronomer Stewart published Demographic Gravitation: Evidence and Applications in which he brilliantly developed a personal interpretation of physics and gravity applied to the study of demography, human behavior and relationships. His research was one of the most important theoretical basis for later studies on the use of gravity in all social sciences, to the extent that it inspired, as mentioned before, Walter Isard himself, to develop a gravitational model applied to trade. The astronomer, in his work, individuated the influence of borders and distance on gravitational models, which reduced the “mutual relationships” of flow in gravity models in many evidences. In this respect, Steward stated that “we might take this sort of thing as evidence that frontiers can produce the equivalent of a large increase in all the international distances, reducing the energies and potentials accordingly” (Stewart 1948, pp. 55–56). McCallum's study has been followed by further research, which applied the gravity model to international economics to compare domestic and international trade. In his analysis of Canadian and U.S. trade, Footnote 16 McCallum (1995) empirically demonstrated that the inclination to trade is higher between neighbouring regions of the same nation as among bordering areas of different states. Although the latter is similar in cultural, legal, and linguistic terms without barriers at the border, it was found that the national border, ceteris paribus, had a negative effect on the exchanges between them. More specifically, McCallum’s study proved that the estimated interprovincial trade between Canadian provinces was 20 times larger (2, 2%) than between the U.S. and Canadian Provinces. The national border effect, which has become known in the literature as the “McCullum Border Puzzle”, has been one of the most discussed topics in international economics. Footnote 17 As a matter of fact, commercial costs increase at the border. There are transaction costs due to customs and other formalities, differences in legal systems, languages and monetary regimes, discrimination through tariffs on foreign products, and other non-quantifiable factors.
In physics, gravity is by definition a multilateral phenomenon, making it suitable for analysing trade relations between many countries, as Isard (1954) initially demonstrated. Nonetheless, the gravity model was initially used as a framework for studying only bilateral trade between two countries, as intended by the theories of Tinbergen (1962) in their standard version. However, the New Economic Geography by Krugman (1991) and the Study of the Effects of Borders by McCallum (1995) brought economists’ attention back to a multilateral approach towards international trade studies. Deardorff (1998a, b, c) believed, for example, that the relative distance of trading partners would influence the volume of trade. Wei (1996), Helliwell (1997), Nitsch (2000) and Chen (2004) developed this approach and defined a variable capable of considering the third country effects. These forces, which are external to two trading partners, are otherwise known as a “third-country effect” and they have been repeatedly studied over time by other authors such as Bang (2006), Blonigen et al. (2007), and Baltagi (2008). Thus, for example, Australia and New Zealand were supposed to trade more with each other at the same distance compared to another pair of countries such as Austria and Portugal, which are close to numerous other countries and markets. This variable was therefore called remoteness. In a pair of partner countries \(i\) and \(j\) , it is defined as follows:
$$where \(z\) is, for country \(i\) , all trading partners other than \(j\) . \(_\) is country \(i\) ’s GDP and \(_\) is the distance between country \(i\) from any commercial partner other than \(j\) .
In the standard bilateral gravitational form, remoteness substitutes Footnote 18 of the constant K of the Eq. (7) which translated in econophysics terms the gravitational constant \(G\) of the formula (2), as follows:
$$Such transposition is theoretically adequate since in physics \(G\) is a constant value throughout the universe. Similarly, in economics, it would be an exogenous variable, given that the whole economic context would influence it. Unlike the cosmic system in the economic system, G can change over time because it is influenced by technological development and historical and social factors of its time. Some agents may influence the division of work, such as the use of the productivity of capital and labour and how they bring process or market innovations. Consequently, the impact of \(C\) would always be multilateral and tend to be constant in the short-term. At the same time, the factors of distance and countries’ GDP would be subject to asymmetric changes, as in the case of new bilateral trade agreements changing the distance between two regions. Unlike in physics, in economics the constant might change with symmetrical adjustments of the entire market taken into consideration. For instance, using digital currencies in the countries involved could positively impact trade by promoting internet purchases. Also, because of this solidity, A is assumed to be constant. Due to this characteristic of universality and consideration of the general context of a market, many economists tend to remove it for simplification or instead lead other researchers to consider it as an element of multilateralism present for a pair of countries, as in the previous formulae. In the economic model, however, remoteness is arbitrary since it describes only the effect of third countries and no other context elements. It represents an attempt to move away from the bilateral model of trade in formula (2), which had historically become the standard gravity model in the study of international trade from a multilateral perspective. Nevertheless, this approach indirectly resumes, logically and practically, the model put forward by Isard (1954). Indeed, by isolating the constant \(k\) in the Eq. (7), the outcome will be similar to the one obtained in formula (11). Footnote 19 Finally, the substitution of remoteness in constant \(C\) , formula (2), represents an effort aimed at introducing a multilateral dimension in a bilateral trade model.
Anderson and van Wincoop (2003) have criticized the remoteness indexes, whose theoretical bases were not deemed correct since they assumed distance as the only factor of resistance to trade. The authors argued that the underlying problem stemmed from physics in the case where a multitude of bodies, forces, and directions are considered. As in the case of remoteness, the scholars studied the multilateral dimension by means of a bilateral trade model, albeit with the promotion of an economic perspective rather than from the point of view of econophysics. Therefore, they focus on territorial boundaries and proceed to assess multilateralism through multilateral resistance. Footnote 20 To this end, they used a gravity model with the consumer’s utility function of the CES type (Constant Elasticity of Substitution) and iceberg-costs. They questioned whether only bilateral transaction costs influenced trade flow, or adjustments due to other countries’ influence were appropriate. Intuitively, the higher the resistance to trade with other countries outside the pair, the more likely the pair is to trade. In this regard, the two economists defined:
According to the two scholars, leaving these factors out of an empirical gravity model makes the econometric estimates inconsistent and biased since it would amount to omitting variables. Multilateral resistance denotes the average resistance to imports and exports trade between a country and any possible trade partner. In practice, focusing only on the bilateral dimension between two countries is no longer possible. It is necessary to move to a multilateral analysis by examining multilateral resistance factors. The latter shows that comparing relative trading costs is far preferable to simply comparing absolute trading costs, as already partially seen in the gravitational model and in the connection that this one has with the comparative advantages in Ricardo (1817). Relative trade costs determine trade, that is, a country's propensity to import from another country based on two ‘resistance’ factors: firstly, with respect to the partner’s imports and, secondly, related to the second country’s exporters. Supposing a country pair is isolated from world markets due to geographic distance, high tariff barriers or other trade costs. In that case, this will result in low multilateral resistances and high trades between the two.
Anderson and van Wincoop (2003) used an empirical cyclical convergence process by trial and error to calculate multilateral resistance. The commercial costs were estimated first in an equation without resistance terms. Then these commercial costs were used to construct a series of multilateral resistances to be inserted into a new regression equation, restoring the new commercial costs. The latter was subsequently reused to build new multilateral resistances, as in the initial phase. The process would repeat itself until the gravity estimates were the same.
In summary, Anderson and van Wincoop’s gravity model can be rewritten as follows (Anderson and van Wincoop 2003: 5–12; Yotov et al. 2016: 15–16):
where \(_\) is the trade flows from exporter \(i\) to destination \(j\) ; \(^\) is the world GDP; \(_\) and \(_\) are the GDP of country \(i\) and country \(j\) respectively; \(\sigma > 1\) is the elasticity of substitution among goods from different countries; \(_\) is the bilateral trade frictions between country \(i\) and \(j\) , which considers various trade variables (bilateral distance, tariffs, currency, regional trade agreements, et cetera); \(_\) is the inward multilateral resistance and denotes importer \(j\) ’s ease of market access, and \(<\pi >_\) is the outward multilateral resistance and represents exporter \(i\) ’s ease of market access. The formula shows the total effects of trade costs in three components ( \(_\) , \(_\) and \(<\pi >_\) ), which creates a wedge between actual trade and frictionless trade. According to all of our theories, bilateral trade flows are determined by more than simply bilateral trade costs and exporter and importer incomes; what also counts is the so-called “bilateral resistance”. This indicates that trade between any two countries is determined not just by their respective incomes, but also by the “cost” of dealing between those countries in comparison to trading with all other countries (Anderson and Van Wincoop 2003)
Adam and Cobham (2007) distinguished multilateral resistance terms (MRT) from bilateral resistance terms (BRT). Looking at a pair of countries, the former would identify the barriers of each of the two countries with the rest of the world; the latter would instead indicate the barriers between the two countries. There would therefore be a compensation effect in a zero-sum game. Basically, Adam and Cobham's distinction is semantic, i.e., it classifies trade barriers between two countries through the terminology of resistance terms. For instance, in the context of the exchange between Italy and France, an increase of the United Kingdom barriers to the exchange, with the same level of BRTIT-FR, would determine a growth of the MRTIT-FR and a consequent intensification of the exchange between Italy and France to the detriment of the exchange with the United Kingdom. Footnote 21 The evaluations of Anderson and van Wincoop consider a multilateral context. In other words, it is not simply considered a bilateral model but one looking at numerous states. Anderson and Van Wincoop modify the model by adding multilateral resistance factors to the bilateral model. However, this has no logical connection either with Isard’s original model, which was already multilateral, or with physics, since to assess the effect of several masses on two masses, multilateral resistance factors are considered, which have no transposition to physics. To that end, adding new and external elements to gravity without conceptual links to the original model is controversial, though it might seem logical.
Anderson and van Wincoop’s model explains international trade from a multilateral point of view by adding multilateral resistance terms to the gravitational model. However, unlike the classic Isard model, which evokes gravity through the transposition of masses and distances to GDP and distances of the countries considered, it does not provide any theoretical transposition of multilateral resistance factors to the force of gravity in physics. There is, therefore, technically no valid motive to continue to use the term ‘gravitational’ to describe an econometric model which, although relevant from the first application of Isard, is no longer inspired by the force of gravity. Footnote 22 It is reasonable to suppose that this trend, evident in most subsequent authors, was used more for historical reasons and for the suggestive power of the term ‘gravity’, rather than to link the two fields of study, thereby losing its original evocative meaning. Furthermore, the multilateral approach can be already observed in Isard’s formula (7), Footnote 23 which summarizes not only the effect of two countries but of a multitude of them on nation \(i\) . Therefore, in a multilateral analysis of the gravitational model, there is no reason to start from the standard bilateral formula presented by Tinbergen (1962) in the equation: \(_= A \frac__>_>\) (Deardorff 1998, p. 9) and transform it econometrically to explain more complex multilateral phenomena without considering that the first transposition of gravity into economics was already, albeit in a theoretical way, multilateral Footnote 24 ; the roots of multilateralism of Isard, however, were not mentioned.
Anderson and van Wincoop (2003) also aimed at answering trade border issues, also known as “McCallum’s border puzzle”, by estimating the gravitational equation using multilateral resistance variables and McCallum's exact specifications and his own dataset. According to them, McCallum's idea of thick boundaries ignored the asymmetric impact of barriers on trade between small and large economies and multilateral protection levels. The results concluded that three reasons could explain the effect on borders: considering the effect of borders by comparing intra-national with international trade; the effect of borders is more remarkable for small nations; the variables not considered push the estimate of effects of the borders to increase. Overall, the authors estimate that borders in industrialized countries reduce trade by an average of 29%. Specifically, as regards Canada and the United States, the scholars found that the border from the Canadian point of view was ten times stronger than that of the United States. With Canada's economy about one-tenth that of the United States, the level of border protection appeared to be a positive function of the economic size of a state. Helliwell (1996) confirmed such results using data from the province of Quebec, which would suffer a disadvantage in the case of potential separation from Canada.
The limits of the multilateral approach of Anderson and van Wincoop, and McCallum before them, in international trade, are manifold. Firstly, as seen in Isard's formula (7), it is unnecessary to look beyond the gravity model to evaluate a multilateral context. The exact opposite is true. Once again, the analysis is affected by its standard econometric approach, overlooking the fact that the application of physics to economics is at stake. Secondly, it would be more appropriate to limit the effect of borders by considering them as part of the distance factor. While not perceiving them sometimes as such—hence the enigma—boundaries are a resistance factor which affects the distance from psychological legal, cultural, and many other points of view. Even when these elements are challenging to identify, it does not mean that they are not there. This observation is partly linked to the problems of endogeneity and reverse causality that can occur due to multilateral resistance factors, when trying to estimate the impact of regional trade agreements (RTA) on trade flows. Countries are likely to form RTAs with partners with whom they have a shorter trading distance. There is not a theory of customs unions that incorporates gravitational forces yet. The closest example is the work of Bikker (1987), who attempted to extend the gravity model to include substitution between trade flows coming from different directions or sources. This would theoretically allow for the analysis of trade production and diversion within inside a gravitational framework. However, this latter lacks a strong theoretical basis and is unable to characterize substitutions between flows. This distance is not only geographical, as previously mentioned, but representative of many proximity variables, such as the legal system, diplomatic relations, language, technological level, colonial heritage, et cetera. While a global, regional analysis requires multilateral terms by definition, it is also true that these terms are not entirely exogenous because they result from the effect of global distances being considered. Consequently, the RTA or MTR elements on the right side of the gravity equation are related to the error term because they depend, in part, on distances. Third, multilateral resistance factors do not explain at first sight which country in a pair will benefit more from a multilateral exchange, as in the case of an agreement with a third country or a new free trade area. Footnote 25 Fourth, evaluating multilateral factors in terms of their individual and combined impact in a multilateral equation is difficult. Finally, it is not logical to explain the border effect through resistance factors that depend on other countries (third-country effect). Borders influence bilateral trade between a pair of countries, regardless of how bilateral trade is affected by surrounding countries simultaneously, thus representing a choice of comparative advantage or opportunity cost. Footnote 26
Before delving into the most recent studies in the field, what follows is a general consideration of the newer models that adopt more sophisticated statistical tools. In this section, judgements on the structure of exogenous variables are made through statistical software packages and a variety of fixed effects. Indeed, since this section aims to provide a general overview, it will not linger on the details of each study. With these premises, the first contribution that will be considered is that of David Huff, professor of Marketing and Geography. Indeed, to estimate market share and retail appeal, he proposed a model that bridges geography and business. This model became popular over the years for its ease of use and applicability to various problems. Market analysts have extensively used it to locate stores, shopping malls, standard models for the industry and other types of retail establishments. The economist and geographer David Huff (1963) re-applied gravity to consumers’ behaviour.
A subject's perceived utility of alternative retail is inversely proportional to its attractiveness. A client's space, for instance, refers to the likelihood that he or she will shop at a specific establishment compared to rivals. This likelihood is determined using distance attractiveness characteristics, as well as the competition. Huff's standard model has no differentiation of goods, no consumer feedback, and no alternative items.. The attractiveness of the retail outlet at location j on consumer demand at location i is defined as:
$$attractiveness\, j= \frac_^>.$$The probability that this consumer demand at location i is satisfied by the store j will be equal, as already seen in Reilly's Eq. (4), to the relative attractiveness of j compared to the attractiveness of other stores. As in Voorhees' model (1956), it is worth recalling that x is an exponent reflecting the effect of distance decay. Hence, total demand is distributed by multiplying expressions (15). Huff, therefore, developed a distribution model of consumer demand in space drawing on Voorhees' model. Voorhees (1956), who was attempting to forecast Baltimore traffic patterns, used gravity to trip distribution. His theory was the first to use the gravitational principle to estimate the number of trips between zones in urban settings. According to gravity formulas, the number of trips is inversely related to distance, and size variables are taken into account for both locations, such as
Voorhees created a distribution model based on such formulas, dividing the estimated number of trips from the origin area by the destination area. This estimation is inversely connected to the required journey time and proportional to the attraction each location exerts. It has the following formula (Philbrick 1973, ibid):
$$where \(_\) is the trip between zone i and zone j, \(_\) is the number of trips generated in zone i, \(_\) is the attraction force of land j, \(_^\) is the travel time between i and j, x is an exponent determined by observation, n is the total number of trips including those directed to j. Similar to the latter, who chooses a spatial distribution of trips based on the attractiveness of the soil, Huff also considers a spatial distribution, which is related to the attractiveness of the commercial area. Huff's probability model is as follows:
$$P_where P is the probability that a consumer at point i goes to the store located in j, is a measure of store attractiveness (such as store size), is the travel time between i and j, x is an exponent determined by observation, n is the total number of stores that also includes the store j. The larger the size of a store, the greater the level of attraction exerted on the consumer. The probability that customers choose that store decreases as distance increases.
However, considering a probabilistic gravity model could be wrong. Indeed, classical econophysics and gravity models follow a deterministic approach with significant simplifications, which seem to be necessary in a heuristic discipline such as economics. This approach has solid neoclassical economic foundations. This latter is based on the concept of general economic equilibrium and mathematical utility maximization, which finds its roots in Newtonian physics. The notion of general economic equilibrium, developed by engineer Léon Walras (1899) and physicist Louis Jean Baptist Bachelier (1900), is a quantitative formulation capable of balancing an economic system's supply and demand equilibrium. Mathematically, equilibrium corresponds to locating the maximum point of a suitable function.
The two scholars conceived it as a physical equilibrium between two balancing forces such as keeping the moon in a stationary orbit around the earth. The resultant of equal and opposite forces is an equilibrium situation for variables endogenous to a system that can be changed only by a change in exogenous variables. The study of gravity models through a probabilistic view poses limits in physics to the determinist approach typical of Newtonian physics and with respect to the neoclassical paradigm, the results of which, although based on simplifying premises, constitute a solid mathematical formalisation for the analysis of economics. Although, therefore, a non-determinist approach based on probability can be very stimulating and intriguing, it will not be explored further in this paper. The reasons are that one needs to find this approach robust for the gravitational tool. Gravity in physics, from Newton to Einstein, is inherently reductionist. It is still so considering that a reconciliation between gravitational interaction and quantum physics has yet to be developed, and although modern physics is leaning more towards a holistic view and has validated Bohr's Atomic Model, the questions raised by Einstein are current and still unsolved. For this reason, the term 'holistic' is inappropriate when referring to a gravitational model. Other physical tools can be more appropriately applied to economics to evaluate probability-based models.
Evenett and Keller (2002) explained that the success of the gravity equation was due to its application to the H–O model and the increasing returns to scale, with the differences in factor endowments and intra-industrial trade explaining the production levels and volumes of international trade. According to them, the data do not theoretically support the assumption of perfect specialization. The H–O model foresees the perfect specialisation of production in different countries but only for large differences in the allocation of factors. In the case of increasing returns, the goods will be more differentiated, as intra-industrial trade will be greater.
Baldwin and Taglioni (2006) identified three errors in order of importance in the theoretical economic derivation of the gravitational model. The first error, called golden, concerns the flawed estimation of the commercial costs due to the failure to consider Anderson and van Wincoop’s multilateral resistance factors or Head’s remoteness effect. This is often the case, because of the scholars’ need for directly observable multilateral resistances. The second error, called silver, refers to the fact that trade should be analysed separately according to its direction at a given moment, and considering that trade from country \(a\) to country \(b\) may not coincide with trade from \(b\) to \(a\) . Finally, the bronze error consists, in the opinion of the researchers, in considering trade flows deflated due to their evaluation based on the aggregate price in the United States.
Helpman et al. (2008), Chaney (2008) and Melitz and Ottaviano (2008) derived the gravitational equation using differentiated goods and constant firm heterogeneity, thus demonstrating the compatibility between Newton’s equation and Melitz’s model. Melitz and Rubinstein (2008) raised the problem of considering the effects of trade barriers on the value of exports and imports and on the entry of exporters. Chaney (2008) calculated this on the supply side, for exports of final goods, continuing the study of Melitz (2003) and assuming asymmetrical countries with different sizes, trade flows, labour costs, and trade barriers. The scholar demonstrated that trade flows have a large margin of adjustment to barriers and that distance effects are determined by the degree of the firm’s heterogeneity, the elasticity of substitution between goods, and the elasticity of commercial costs to distance. Therefore, the effect of distance on trade flows will not only depend on the elasticity of substitution between goods but also on the degree of the firm’s heterogeneity. Helpman et al. (2008) examined the demand side, verifying trade barriers and policies’ impact on flows. They developed a selective gravitational model, which provided both positive and zero bilateral flows between pairs of countries due to selection and business competition. The model involved two phases in two equations. First, a pair of countries decide whether it is convenient for them to trade or not (extensive margin); second, they decide on the volume of exchanges (intensive margin). According to Helpman, the recent increase in world trade is mainly due to intensifications in the exchanges of traditional trading partners. Egger and Pfaffermayr (2011), in their structural estimation of the gravity model with path dependence of country-pair level exporter status, pointed out to this persistent effect in a study, which stated that 66% of the pairs of countries that made exchanges three years earlier still exchanged with each other. Furthermore, the 20% of couples with zero exports also had no exports 3 years earlier, and only 13% showed a significant change in the average levels of trade in 3 years. According to Egger and Pfaffermayr, access to a new commercial market required entry costs (sunk cost), which would favour traditional exchanges. They also submitted that the third country effect on the exchange rate in a pair of countries would imply, albeit adding a certain delocalization effect on the business side, a positive flow variation in the country chosen by the company as the new location and a negative variation in the country of origin of the enterprise. This last point should be given a lot of weight. It can be placed in a geographic economy through the choice of location for an economic agent, which according to the authors depends on the comparison between the costs of exchange with one country rather than another.
Anderson and Yotov (2010) introduced a sectoral gravity model to estimate the trade of specific commodity classes and multilateral resistance variables by equating fixed effects with structural gravity counterparts. Yotov (2012) analysed the effects of globalization on the reduction of costs related to trade using the gravity model, dividing between the costs of trade within countries and costs of international trade. According to him, globalization leads to a decrease in the costs of international trade compared to the costs of domestic trade, and to a consequent decrease in the thickness of McCallum's borders. Olivero and Yotov (2012) proposed a dynamic theoretical gravity model for prediction with asset accumulation in the presence of panel data, in which exchange values were delayed as regressors. They observed a “commercial persistence” that included a delayed decline in gravity patterns. Indeed, over time there would be a “persistence effect of protection” of positive trade barriers through the accumulation of capital, which would be marked by an increase in the country's production, as well as in its mass, and consequently in international trade. The researchers also showed that multilateral resistance effects should be considered as fixed effects over time.
Arkolakis et al. (2012) analysed the situation where trade is balanced, profits are a constant share of GDP and the import demand system is CES, thereby showing that a large class of quantitative trading models generate isomorphic gravity equations (equivalent in structure between them) with respect to gains from trade. Therefore, the gravitational model can calculate the welfare gains from trade in international economics.
Recent research has focused on the end of the gravity model, as well as on the transposition from the sphere of physics to the virtual sphere, and on the less tangible flow of goods. Footnote 27 Therefore, this branch of studies has interested the economic literature. As discussed, the gravitational model in particular has recently moved its interest in social sciences from the study of flows of things towards that of less tangible things. With regard to this, Castells (1996) has applied the concept of “space of flows”, and, Batty (1997) and Gorman and Malecki (2000) have introduced the areas of “cyber geography” and “virtual geography” with the aim of describing a new virtual space, which extends beyond the geographical one. Trade studies have also concerned complex systems and, inevitably, also digital networks. On the one hand, the interest of scholars has focused on the impact of digitalization on the different forms of distance, including the physical one (Reggiani et al. 2010; Tranos 2011). On the other hand, the consequences of economic and geographical distance on the digital arena have been at the centre of attention (Simini et al. 2012; Newman 2003; Watts 2004).
Nonetheless, Cairncross (1997) has questioned the application of the gravitational model to trade as he put forward the concept of “death of the distance”. Along the same lines, the notion of “flat world” by Friedman (2005) suggests the inexistence of distances, thereby implying the disappearance of income and wealth as factors of concentration. Footnote 28 Admittedly, overlooking distance would mean, from a gravitational perspective, also a diminished concentration force of the masses. This could be transposed in macroeconomics terms as a reduction of wealth since the masses can be comparable to the GDP of nations (their total income). Therefore, the absence of concentration results in perfect distribution. It follows that the gravity model would end if the “death of distance” was considered.
In this regard, Vozna (2016) examined the market through the lens of entropy to determine richness. This approach stems from Wilson (1970), who applied the notions of entropy and the “law of diminishing returns in economics”, intended as dispersion of resources and gains in productivity. Wilson’s entropy of urbanization is similar to the one introduced by Vozna with respect to dispersion of wealth. In spatial terms, the dispersion of profit can be associated in the real world with the notion of dispersion of wealth. The same applies to the concept of equality both in the field of capital among economic actors, and among subjects of different countries. It is, therefore, unsurprising that equality and dispersion dominate in the absence of distance (the latter having a single value). According to such model, the maximum of entropy generates a more competitive market. It could be argued that such analogy associating capital and distance is forward-looking. Indeed, in macroeconomics, in the long-run, profit is equal to zero in the case of perfect market competition. It follows that the “cold death of the Universe”, which is obtained with the maximum entropy in the context of physics, may be related to the already mentioned “death of distance”. Footnote 29 In both cases, there seems to be opposition to the gravitation model on the one hand, and to the economic notions of concentration of wealth and income on the other hand. Footnote 30 As a consequence, a “flat world without distance”, which entails a diminished concentration of income and wealth, originated in a perfect market equilibrium. Recently, scholars in the field of technological progress and digitalization have suggested that distance is economically relevant in the current world. This is because of the increased diversity and complexity of society and space, where access to the internet is diversified in accordance with its literacy and diffusion. However, Rietveld and Vickerman (2004) argued that the hypothesis of “death of distance” is untimely. Indeed, travel is not yet a disadvantage, and furthermore, the diversified preferences for goods and activities could be related to increasing real incomes. Moreover, the transformation of activities and transport models can influence the choice of residence, family, work, and leisure time. To conclude, McCann (2008) combined the notion of “flat world” with the one of “curved world” aiming at overcoming restricted perspectives under the aegis of Economic Geography, which brings together globalization and localization. As seen before in this paper, Tranos and Nijkamp (2013) applied digitalization to the gravity model. Tranos and Nijkamp (2013) were therefore able to overcome the new reality of cyberspatial and distance on the internet by applying digitalization to the gravity model. Disdier and Head's (2008) thorough meta-analysis of 103 studies and 1467 estimated friction elasticity values in gravity analysis with a negative "power function", showing that the distance friction, i.e. elasticity's absolute values β, and the volume of trade flows have an inverse relationship, as shown by their weighted arithmetic mean (0.855) and arithmetic mean (0.907). Moreover, the scholars reveal that the effect of distance tends to grow over time, as shown by the growth of β the as it can be seen in the Fig. 2.
These findings contradict the hypothesis that technological advancement and information and communication technology (ICT) have diminished distance’s role in spatial connections. Footnote 31 In doing so, we can conclude that the gravity models still have a “raison d’etre” in the modern world, not disappearing in the face of new circumstances but changing over time.
In economics, the question of a flat world can be viewed econophysically as in the formula (18). The commercial interchange would expand exponentially at a distance close to zero. Indeed, the concept of globalization has caused exports to increase on a global scale continuously. A challenge that may be the inverse of the death of distance is the problem of trade flows between countries being equal to zero. Zero gravity does not exist in nature. However, there are places in the cosmos that are very remote from astronomical sources where gravity is feeble, or there are points of balance between forces.
$$flat world: \underset<_<\mathit>\to 0><\mathrmThis paper has covered the existing theoretical formula around the gravitational model from its origins to the present time. The principal authors have been critically reviewed, from discussions around the first theoretical model in social science in trade to the multilateral and digital economy models. The implications and deep roots of the model in international trade flows have been widely discussed. The gravitational model’s strength in competitive and oligopolistic markets has been demonstrated.
What emerges is that the gravity equation represents a suitable analysis framework for multiple models and markets. This is true for bilateral and multilateral perspectives. Wide attention has been given to the study of Walter Isard, theorist of the gravitational model in economics, with a complex description of his approach and discipline. It should be noted that the models examined did not always treat Isard’s formulation with an orthodox or econophysics approach. A discussion of the fact that the scholar has been wrongly neglected in the gravity model literature was also conducted, showing how this error was the cause of several subsequent theoretical simplifications.
The major evolutions of the model has been considered, and an attempt was made to summarise their usefulness, sometimes criticising their deviations. An approach to physics has been preserved. The link between the model and economic geography was also underlined. The relevance of the theory for the area of econophysics has been considered, and discussions were made about the birth of the model in physics and its application to economics. In this respect, Tobler’s first law of geography was also illustrated for its great transversality. The latter is more general and straightforward than the gravity equation, which is an aspect well worth noting. In most of the developments in the gravitational model seen in economics, it has been found that these evolutions transcend gravity, its background, and the genesis in physics. They are, in fact, more similar to Tobler’s first law of geography applied to economics or to econometric modelling of reality, rather than to the attracting forces in trade or an econophysical link to Isard’s original model. In these studies, the word ‘gravity’ continues to be employed for its historical and suggestive power, but no longer for its real meaning, since these evolutions being in essence, advanced stand-alone models. Over time, various econometric evolutions of the gravity model have been introduced to explain variables which were not addressed in the original model. This has further refined its predictive value and broadened its scope. In this regard, therefore, these evolutions of the model go well beyond econophysics. Indeed, they are suitable frameworks of economic geography for the study of space in economics by means of the “friction of distance” or Tobler’s first law of geography.
Contrary to this background, the concept of distance in the gravity model has acquired greater relevance concerning the notions of “flat word” and “death of distance”. The focus of the recent literature on globalisation and digitalisation as the applications of gravity to economics has been analysed with closer attention to the concept of ‘entropy’. Finally, the need for future authors to expand upon Isard’s work and integrate economic geography with international economics using the gravitational model was discussed. However, it has been highlighted that this path was not entirely ‘new’ in literature but was present since its inception. Related themes and elements were new economic geography, multilateral resistance factors (MRT) and the border puzzle, whose strengths and weaknesses have been reviewed. In conclusion, Isard's theoretical analyses and his raised issues are still relevant and have not been completely resolved. From the above, it follows that no evolution of the gravitational model in literature is yet capable, in its multilinearity, of an effective synthesis between economic geography and international trade, with the ability to create a “superior theory of international trade”, as Isard had sought to elaborate. Therefore, further efforts in this direction would be desirable.
As this article is a literature review, no new data were generated or analyzed in this study. All information sources used in this study are cited appropriately in the reference list.
Usually is a constant of proportionality, but in several situations, is used to indicate the alternative in the world market. If a country has many alternative partners, it will tend to trade little with each by splitting its flows is a constant in Feenstra (2016). According to Yotov et al. (2016: 17), is the inverse of world production (1/Y world).
Economic masses are not limited to identifying only a couple of countries, but they can also be used to analyse the exchange between free trade areas, cities, regions, single markets such as the EU or economic zones such as South America or Southeast Asia. Other scholars treat it as the aggregate expenditure of a country rather than as its GDP (ibid).
Like Reilley, Stewart considers straight line distances, while providing several examples where distance should be otherwise interpreted.
A significant number of papers in the literature reports this misleading information, which I find incorrect.
Analogy with Newton's law of gravity model: just as the gravitational attraction between two objects is proportional to the product of their masses and decreases with increasing distance, trade between two countries is proportional to the product of their GDP and decreases with increasing of their distance.
Isard speaks of ‘economic distance’, which must consider the relative movement of goods on different means of transport.
Indeed, at the time of Isard, several scholars had already tried to develop a model of multilateral international trade; among these are Machlup (1943), Frisch (1947), Metzler (1950), and Hansson (1952).
The attentive reader will not be surprised, indeed, that Tinbergen is considered to have been one of the founding fathers of econometrics (Magnus and Morgan 1987: 117–142).
The interested reader is addressed to Tobin (1997) and to Dekker (2021).Moreover, in gravity models, the idea of determinism in human beings’ actions must be accepted to some extent. Indeed, in an econophysical gravity model, human interactions must be governed by universal laws.
Tobler and Wineburg (1971) using the gravity model estimated the unknown locations of several Assyrian settlements for which commercial data between 1940 and 1740 BC were available. According to the first law of geography, the idea was that the more settlements traded with each other, the more similar they were in terms of position (Tobler and Wineburg 1971).
Beyond the proposed conceptual division between ‘structural gravity’ and ‘gravity’ as a simple tool for calculating a flow (the latter being more similar in a certain sense to a distance decay spatial model), it is worth remembering that Tobler had also drawn inspiration for his law from gravitational models using an econophysics approach contributing greatly to other works and to the development of the gravitational metaphor. Indeed, the geographer (1970) also developed a reverse gravitational model capable of deriving the position from interactions. In doing so, he was reversing his law with flows, such as data values and distance, as an unknown variable, thereby creating a tool for analysing not only flows, but also society. He stated that: “all things can be located on a map so that similar things are brought closer than less similar things” (Tobler 1970:537–542). In addition, a few years later in another brilliant work (Spatial Interaction Patterns, 1975) the scholar enriched the gravitational model of structural and logical elements using mathematical and vector calculus, demonstrating a thorough understanding of physics.
This should also help understand Isard’s ambition to develop a superior theory of international economics, which integrates the theories of commerce with those of localization in economic geography. Isard, founder of the gravity model in economics, is also credited with founding regional science. It is no coincidence that the gravity model is a tool for spatial analysis, industrial location, urban development and international economics. However, few scholars have really understood this comprehensive potential.
See more in: (1) Yotov et al. (2016: 12); (2) Anderson (2011: 1).The interested reader about this “fortunate empirical validity” is referred to Reinert et al. (2009: 568).
McCallum used data on interprovincial and international trade by Canadian provinces for the period 1988–1990.
Feenstra (2002), Cheong, and Kwak (2015), Magerman, Studnicka, and Van Hove (2016) and Carter, and Goemans (2018).
The interested reader can find mathematical passages in: Head, Keith (2003: 2–4). Mathematically, \(k=Scholars report significant differences in the definition of remoteness and gravity obtained through multilateral factors of resistance. According to them, remoteness is a non-theoretical measure and an inadequate attempt to monitor multilateral resistance (Anderson 2011: 3).
United Kingdom, which in this case represents the rest of the world.As already discussed, the first application can be traced back to Tinbergen. Moreover, at this point, it would be more accurate to speak of multilateral resistance terms, for example in Tobler’s first law of geography model applied to trade.
Isard (1954: 305–320) had already uncovered the need for a multilateral study of international trade, which was already taken into account in his formula of gravity.
The economic modelling started with the subsequent simplified formula by Tinbergen (2.1).Dai et al. (2014) considered the deviation effects of free trade agreements through the gravity equation, outcomes that FTAs divert trade within the parties of the agreement and disadvantage countries that are not members of it.
The choice made will give a precise direction to trade flows, as we have already seen in Ricardo and for some aspects in Smith.
At the end of the twentieth century, the economic debate was focused on the pivotal role played by globalisation and digitalization and, in particular, on a major consequence of these phenomena which is the lack of borders among the countries. Even though McCallum (1995) demonstrated the economic relevance of national borders by empirically using the gravity equation, the idea of a world without borders has never abandoned the economic debate.
It should be noted that Samuelson (1949) had admitted the presence of transport costs and the limits in achieving stronger economies of scale (in a restricted market with the value of transportation costs’ different from zero) as to illustrate the motives behind differences in wages across nations. Indeed, the lack of such costs allows the equality of wages in a model composed of two countries.
William Thomson, a British physicist, introduced the notion of “cold death of the Universe” in 1851. Such expression refers to the energy’s distribution in space in a uniform way, which was generated by dispersion. Therefore, from a practical point of view, the universe’s equal temperature created the conditions for maximum entropy. As a result, all the processes of energy, such as life, could not occur anymore. It may seem counterintuitive to consider a level of maximum entropy when the distance is zero. Indeed, in physics, a distance equal to zero leads to maximum concentration (big bang). However, in economics, considering Vozna’s case, entropy is measured in terms of wealth, so we will observe that a reduction in distance leads to a better distribution of wealth and a more competitive market where profits, but also average total costs, are minimized. We are going to have zero profit in the long run for individual companies, but we are also going to reach the point of maximum exchange and maximum profit for the economy as a whole, as in the formula (18).
Both in physics and in economics, the gravity originating from the mass is the force of attraction and concentration. Nonetheless, distance is the resistance factor that balances the concentration force. It results that entropy and distance are interrelated, given that the maximum dispersion and entropy of the masses occurs with greater distance among them.
For more investigation, the interested reader is referred to chapter two of Buciuni and Corò (2023) “The World is not Flat: Developments and Processes of Polarization”.
I thank Prof. Adalgiso Amendola (University of Salerno) and Prof. Sami Bensassi (University of Birmingham) for their support and helpful discussions.
Open access funding provided by Università degli Studi di Trieste within the CRUI-CARE Agreement. The author was solely responsible for the design, execution, and analysis of the study. No external funding organizations supported this research.
The author is solely responsible for the design, execution, and analysis of the study.
The author has no conflicts of interest to disclose.
This article does not contain any studies with human participants performed by the author.
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Capoani, L. Review of the gravity model: origins and critical analysis of its theoretical development. SN Bus Econ 3, 95 (2023). https://doi.org/10.1007/s43546-023-00461-0
Anyone you share the following link with will be able to read this content:
Get shareable link
Sorry, a shareable link is not currently available for this article.
Copy to clipboard
Provided by the Springer Nature SharedIt content-sharing initiative